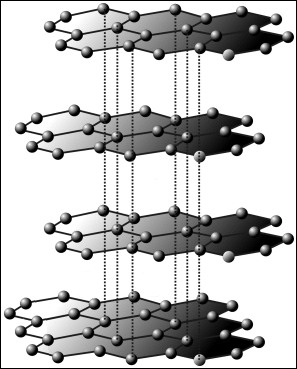
Dr. Ivan Fernandez-Corbaton from the Institute of Nanotechnology at the KIT presented his research in our CRC seminar April 21st. We are very happy to share his own short recap of his exciting talk on the question “How Electromagnetic Chiral is a Chiral Object?” with you:
Dr. Ivan Fernandez-Corbaton:
‘Take an object and place it in front of a mirror. If the “being in the other side of the mirror” handed you their version of the object, there are two possibilities: You can rotate it so that it is now identical to your original object, or you cannot. If you cannot, the object is called chiral. Try it at home with a wine opener and you will see that you will never be able to superimpose the two helices because they twist in opposite senses, as the two seashells in the picture.
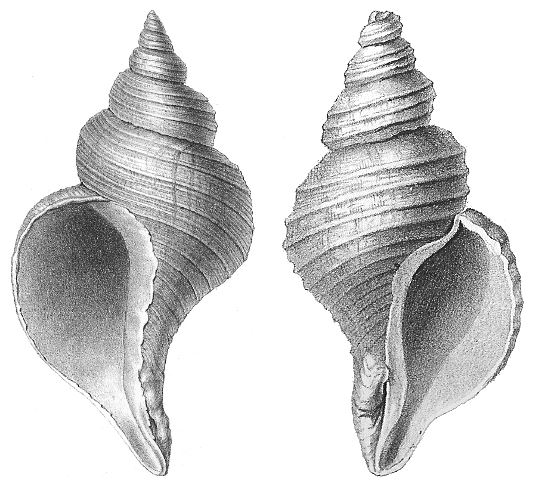
These seashells are chiral. Source: Wikipedia.Org
Chirality is entrenched in nature: From the weak interactions between elementary particles to the empirical fact that most of the building blocks inside the human body are chiral (aminoacids, proteins, the DNA strands and many more).