In June 2016 we, Christine Grathwohl, Fabian Hornung and Luca Hornung, had the opportunity to participate in the summer school “Harmonic Analysis at its Boundaries” in Nantes. The aim of this event was to present recent advances in abstract and applied harmonic analysis in depth through three minicourses and to give an overview about connected topics through accompanying talks.
The origins of the harmonic analysis go back to the end of the 18th century. One of the founders of this theory was the French mathematician Joseph Fourier, who developed it during his attempts to solve differential equations. Nowadays applications are found in various fields of science and technology, reaching from acoustics and optics over signal processing till cryptography.
Consider for example a music song that you want to record as an MP3 file in such a way that you need as low memory capacity as possible. All the information on frequencies that are not in the frequency range that can be heard by us humans is not needed. It is impossible to delete this information directly from the signal caused by the air pressure in the microphone. Instead of this, one computes the Fourier transform of a signal that divides the information on the different frequencies. Now the very high and very low frequencies can be cut off easily and a retransform gives the desired result.
In the following, we want to give an insight into the topics of the minicourses mentioned above. A little cautionary reminder: this short report requires knowledge of some advanced mathematics.
Roughly speaking, wave turbulence describes energy transfer between different frequencies in the nonlinear interaction of waves. In mathematical terms, this can be measured by the growth of Sobolev norms in time. Patrick Gérard studied in his minicourse “Hankel operators, the cubic Szegő equation and wave turbulence” the cubic Szegő equation
$$
i \partial_t w=\Pi_+ \left(\vert w\vert^2 w\right)
$$
on the torus \( \mathbb{T} \), where the Riesz-Szegő projection \(\Pi_+\) is given by \(\Pi_+ u(x)= \sum_{k\in\mathbb{N}}\hat{u}(k)e^{ikx} \) for \(u\in L^2(\mathbb{T})\) and \( x\in\mathbb{T}^{d}\) . This equation approximates the cubic half wave equation
$$
i \partial_t u+\vert D\vert u=\vert u\vert^2 u
$$
for small initial values \(u_0\) satisfying \(\Pi_+ u_0=u_0\), where \(\vert D\vert\) is defined by \( \vert D\vert u= \sum_{k\in\mathbb{Z}} \vert k\vert u_k e^{i k x}\). The half wave equation is a toy model for nonlinear wave propagation without dispersive effects. Compared to the nonlinear Schrödinger equation, this lack of dispersion comes from replacing the Laplacian by the first order operator \(\vert D\vert\).
Now we return to some properties of the Szegő equation. The conservation laws
$$
\Vert w(t)\Vert_{L^2}^2=\operatorname{const.}\qquad\text{ and }\qquad \left(D w(t),w(t)\right)_{L^2}=\operatorname{const.}
$$
yield global wellposedness with norm conservation in \(H^\frac{1}{2}(\mathbb{T})\). However, for \(s> \frac{1}{2}\) we only have an exponential growth of the \(H^s(\mathbb{T})\)-norm in time. This leads to the question whether the Sobolev norms really grow fast and whether the solutions become turbulent in the longrun.
The answer is given by the close connection of the Szegő equation to so called Hankel operators. If we link the solution \( w(t) \) of the Szegő equation with the linear operator \( H_{w(t)}\) on \( L^{2}(\mathbb{T}) \) defined by \(H_{w(t)}(b)=\Pi_+\big(b \overline{w(t)}\big)\), we can derive the evolution formula
$$
H_{u(t)}=U(t)H_{u_0}U(t)^*
$$
with unitary operators \( U(t)\). This yields many correspondences between operator norms for \(H_u\) and norms for \(u\), like \(\Vert H_u\Vert_{HS} \eqsim \Vert u\Vert_{H^\frac{1}{2}}\). Also, there is an explicit formula for the solution of Szegő equation in terms of \(H_u\), the Fourier transform and the shift operator on \(l^2\).
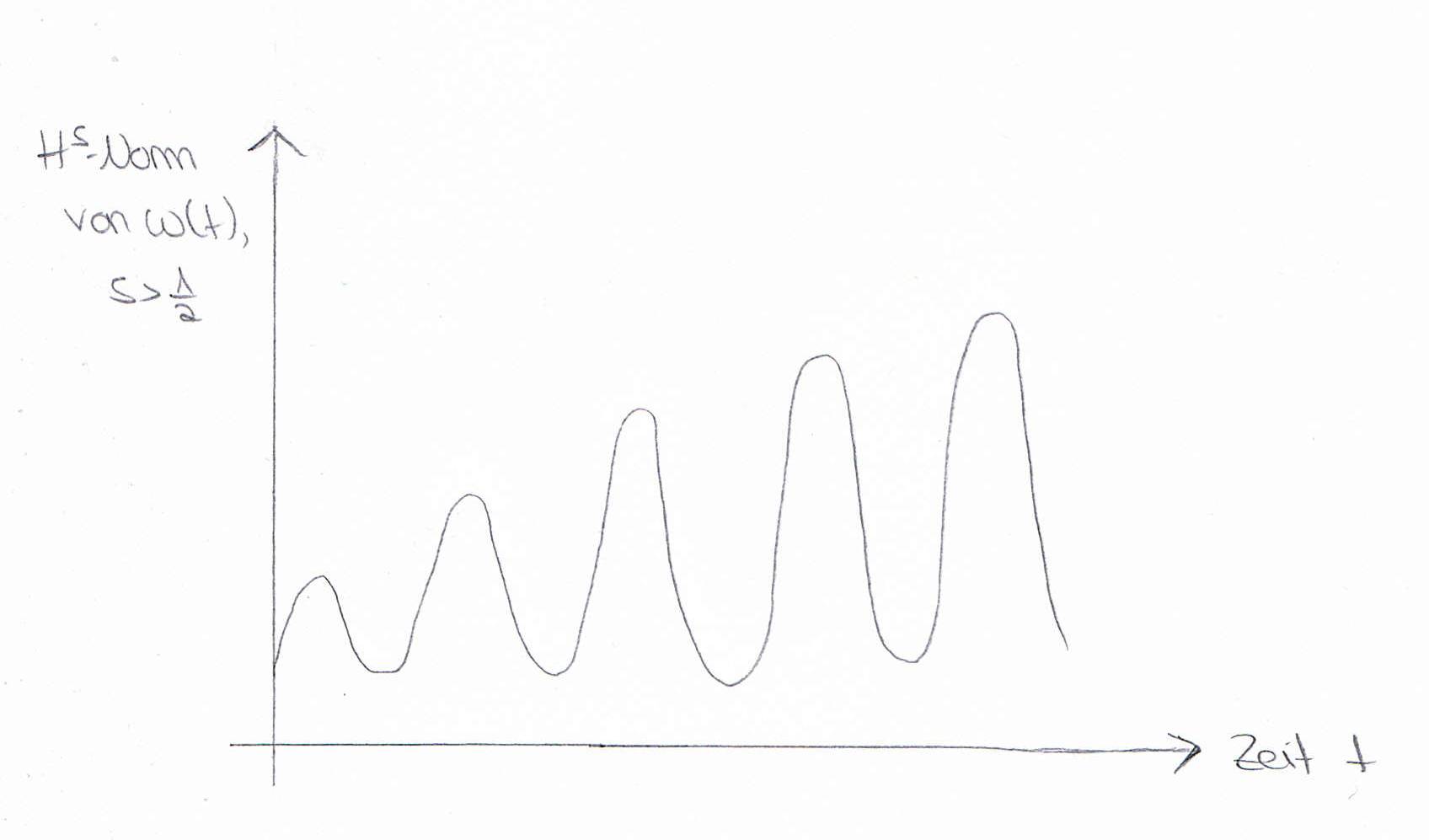This identity allows to reduce the study of the solutions to the classical spectral theory of the compact operators \(H_{u_0}\) and finally gives the following answer to the question above. For every \(s>\frac{1}{2}\) the \(H^s(\mathbb{T})\)-norm of the solution tends to infinity with superpolynomial growth at some sequence of times, whereas it returns to the initial condition at another sequence of times, both tending to infinity. Indeed, the behaviour of the solutions of the cubic Szegő equation is very turbulent.
The two other minicourses dealt with a very classical subzone of harmonic analysis, the derivation of very precise estimates. Tuomas Hytönen presented in his lecture “Sharp norm estimates for singular integrals” the recent development on sharp weighted \( L^{p}\)-estimates of Calderon-Zygmund operators based on his own celebrated \( \operatorname{A}_2\)-Theorem. Unfortunately, as far as we know, there are no direct applications of these results to partial differential equations or as he said afterwards “applicability is always a tricky issue”. Anyway, the presented techniques gave us a completely new perspective of singular integral operators.
A Calderon-Zygmund operator is an \( L^{2}(\mathbb{R}^{d})\)-bounded singular integral operator \( T \) of the form
$$
Tf(x)=\int_{\mathbb{R}^{d}}k(x,y)f(y)\operatorname{dy}
$$
related to a kernel \( k:\mathbb{R}\times\mathbb{R}\setminus\{x=y\} \) that satisfies the growth estimate \( |k(x,y)|\leq C|x-y|^{-d} \) and additionally some cancellation conditions. These ensure that \( T \) extends to a bounded operator on \( L^{p}(\mathbb{R}^{d})\) for all \( 1<p<\infty \). Note that this extension property is not immediate at all, since classical approaches as a Schur test fail due to lack of integrability of \( k \).
In the last decades, the study of these operators has found many applications in regularity theory for elliptic PDE. For instance, one has \( \partial_i\partial_ju=R_iR_j(\Delta u) \) for \( i,j=1,\dots,d \), where the Calderon-Zygmund operator \( R_i \), the so called Riesz transform, is given by
$$ R_iu(x)=\int_{\mathbb{R}^{d}}\frac{x_j-y_j}{|x-y|^{d+1}}f(y)\operatorname{dy}. $$ Therefore, the boundedness of \( R_i \) on \( L^{p}(\mathbb{R}^{d}) \) for \( 1<p<\infty \) implies that the domain of \( \Delta \) on \( L^{p}(\mathbb{R}^{d}) \) is indeed \( W^{2,p}(\mathbb{R}^{d}) \). Note that this fails for \( p=1 \) and \( p=\infty\) since the Riesz transform is not bounded on \( L^{1} \) and \( L^{\infty}\) .
About 40 years ago people began to study Calderon-Zygmund operators on weighted \( L^{p} \)-spaces and it turned out that the class of Muckenhoupt weights \( A_p:=\{\omega:\mathbb{R}^{d}\to(0,\infty)|[\omega]_{A_p}<\infty\} \) with \( A_p \) constant and the definition
\[ [\omega]_{A_p}=\sup\limits_{\text{cubes }Q\subset \mathbb{R}^{d}}\Big(|Q|^{-1}\int_{Q}\omega(x)\operatorname{dx}\Big)\Big( |Q|^{-1}\int_{Q}\omega(x)^{-\frac{1}{p-1}}\operatorname{dx}\Big)^{p-1} \]
allows to prove boundedness of \( T \) on \( L^{p}(\mathbb{R}^{d},\omega) \) for all \( 1<p<\infty \) and \( \omega\in A_p\). However, for a long time the optimal dependence of \( \|T\|_{L^{p}(\mathbb{R}^{d},\omega)} \) on \( [\omega]_{A_p} \) was unknown in case of general Calderon-Zygmund operators until Hytönen proved in 2012 that for \( p=2 \) the norm of \( T \) depends linearly on \( [\omega]_{A_2}\). In his minicourse, Hytönen presented the refined estimate
\[ \|T\|_{L^{p}(\mathbb{R}^{d},\omega)}\leq C_d[\omega]_{A_p}^{\max\{1,(p-1)^{-1}\}} \]
for \( 1<p<\infty \) and \( \omega\in A_p \) with a constant \( C_d>0 \) only depending on the dimension \( d \). Since the proof was very technical, we just want to mention the most difficult step, a pointwise domination of \( Tf \) for a given smooth function \( f \) by averages of \( f \). To be precise, we have
\[ Tf(x)\leq C \sum_{Q} \mathbf{1}_{Q}(x)|Q|^{-1}\int_{Q}f(y)\operatorname{dy} \]
for all \( x\in\mathbb{R}^{d} \) and a constant independent of \( f \), where the sum is taken over a so called sparse collection of disjoint dyadic cubes. Although this collection of cubes depends on \( f \) , this decomposition is still very useful and, at least for us, quite surprising.
In contrast to Hytönen, the last main speaker, Michael Christ, investigated a concrete inequality, the Hausdorff-Young inequality. It is well-known that the Fourier transform \( \mathcal{F} \) is bounded on \( L^{2}(\mathbb{R}^{d}) \) and bounded from \( L^{1}(\mathbb{R}^{d}) \) to \( L^{\infty}(\mathbb{R}^{d}) \) with norm one. As a consequence, by complex interpolation, we get \( \|\mathcal{F}f\|_{L^{q}(\mathbb{R}^{d})}\leq \|f\|_{L^{p}(\mathbb{R}^{d})} \) for all \( f\in L^{p}(\mathbb{R}^{d}) \) with \( p\in[1,2] \) and \( 1/p+1/q=1 \). For \( p\in(1,2) \) this can be improved to \[ \|\mathcal{F}f\|_{L^{q}(\mathbb{R}^{d})}\leq p^{\tfrac{p}{2}}q^{-{\tfrac{q}{2}}} \|f\|_{L^{p}(\mathbb{R}^{d})} \] and this estimate is known to be optimal with equality if and only if \( f \) is of Gaussian type, that is \( f(x)=e^{-\pi |x|^{2}} \) or an affine transformation of this function. At the summer school, Christ presented his recent refinement. He proved \[ \|\mathcal{F}f\|_{L^{q}(\mathbb{R}^{d})}\leq \Big(p^{\tfrac{p}{2}}q^{{-\tfrac{q}{2}}}-\frac{\operatorname{dist}_p(f,\mathcal{G})^{2}}{\|f\|_{L^{p}(\mathbb{R}^{d})}^{2}}\Big) \|f\|_{L^{p}(\mathbb{R}^{d})} \] for \( p\in(1,2] \), where \( \operatorname{dist}_p(f,\mathcal{G})\) is the distance of \( f \) with respect to \( \|\cdot\|_{L^{p}(\mathbb{R}^{d})}\) to the set of all functions of Gaussian type. This means that the estimate improves if \( f \) is far away from being a Gaussian. Unfortunately, the proof is technically involved and needs methods like additive combinatorics that are fare beyond the scope of this blog. So, we stop at this point and thank everyone who is still reading this last sentence.